I have previously been subject to professional plagiarism, as I have described on my other blog:
Unacknowledged re-use of intellectual property
However, I was not expecting to have my wine blog plagiarized. Sadly, this has now happened, too. There is a Blogspot blog, called "artsforhealthmmu" that, as of today, consists entirely of copies of 19 of my posts from the Wine Gourd, without an iota of reference to me or my blog. Needless to say, I am not going to put a link to that blog here, but you will find it if you search for the name on the web.
It is not immediately obvious what the game is, here. That other blog is well designed, and there is currently no advertising or rogue links that I can find, although that may change. Interestingly, there is a genuine site called the "Arts and health blog" that has almost exactly the same web address as the plagiarizing blog. (The latter has an extra "s" in the address.) So, there are other people who seem to be as much a victim of this situation as I am.
I have submitted a request to Blogger to have the offending blog removed, but that will take some time to implement. I am hoping that this will result in a better resolution than happened the last time I was plagiarized (mentioned above), where the offending (well-known) author had no real excuse or apology, and the (well-known) book publisher metaphorically just shrugged his shoulders. A pox on all of them!
Update 4 Nov.:
Notice from Google:
"In accordance with the Digital Millennium Copyright Act, we have completed processing your infringement notice. We are in the process of disabling access to the content in question"
Monday, October 30, 2017
Monday, October 23, 2017
Ranking America’s most popular cheap wines
In a recent article in the Washington Post, Dave McIntyre contemplated 29 of America’s favorite cheap wines, ranked. Here, he looked at some of the mass-market wines available in the USA, and tried to decide which ones might be recommendable by a serious wine writer.
To do this, he "assembled a group of tasters to sample 29 chardonnays, cabernets and sweet red blends that are among the nation’s most popular, plus a few of my favorite and widely available Chilean reds". He then ranked the wines in descending order of preference (reds and whites separately), and provided a few tasting notes.
This is a risky business, not least because the tasting notes tended to be along the lines of "smells of sewer gas" and "boiled potato skins, sauced with rendered cough drops", which might suggest that the exercise was not taken too seriously by the tasting panel. However, a more important point is that the general populace of wine drinkers might not actually agree with the panel.
The latter point can be evaluated rather easily, by looking at any of those web sites that provide facilities for community comments about wine. I chose CellarTracker for this purpose. I looked up each of the 29 wines, and found all but three of them, the missing ones being some of the bag-in-box wines. For each of the 26 wines, I simply averaged the CellarTracker quality scores for the previous five vintages for which there were scores available (in most cases there were >50 such scores).
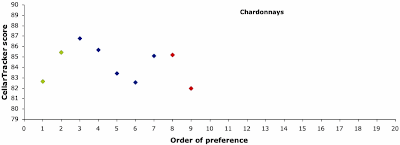
I have plotted the results in the two graphs above, where each point represents one of the wines. McIntyre's preference ranking is plotted horizontally, and the average CellarTracker scores are shown vertically. McIntyre's Recommended wines are in green, and the Not Recommended wines are in red.
It seems to me that there is not much relationship between the McIntyre ranking and the CellarTracker users' rankings. In particular, there is no consistent difference in CellarTracker scores between those wines that McIntyre recommends and those that he rejects. In other words, the preferences of the populace and the preferences of the tasting panel have little in common.
So, what exactly was the point of the Washington Post exercise? It may be a laudable exercise for wine writers to look at those wines that people actually drink, rather than those drunk by experts (eg. Blake Gray describes it as "outstanding service journalism"). However, we already have CellarTracker to tell us what actual wine drinkers think about the wines; and we have a bunch of specialist web sites that taste and recommend a wide range of inexpensive wines (see my post on Finding inexpensive wines). These sources can be used any time we want; we don't need a bunch of sardonic tasting notes from professionals, as well.
Personally, I would go with the CellarTracker scores, as a source of Recommended wines.
To do this, he "assembled a group of tasters to sample 29 chardonnays, cabernets and sweet red blends that are among the nation’s most popular, plus a few of my favorite and widely available Chilean reds". He then ranked the wines in descending order of preference (reds and whites separately), and provided a few tasting notes.
This is a risky business, not least because the tasting notes tended to be along the lines of "smells of sewer gas" and "boiled potato skins, sauced with rendered cough drops", which might suggest that the exercise was not taken too seriously by the tasting panel. However, a more important point is that the general populace of wine drinkers might not actually agree with the panel.
The latter point can be evaluated rather easily, by looking at any of those web sites that provide facilities for community comments about wine. I chose CellarTracker for this purpose. I looked up each of the 29 wines, and found all but three of them, the missing ones being some of the bag-in-box wines. For each of the 26 wines, I simply averaged the CellarTracker quality scores for the previous five vintages for which there were scores available (in most cases there were >50 such scores).
I have plotted the results in the two graphs above, where each point represents one of the wines. McIntyre's preference ranking is plotted horizontally, and the average CellarTracker scores are shown vertically. McIntyre's Recommended wines are in green, and the Not Recommended wines are in red.
It seems to me that there is not much relationship between the McIntyre ranking and the CellarTracker users' rankings. In particular, there is no consistent difference in CellarTracker scores between those wines that McIntyre recommends and those that he rejects. In other words, the preferences of the populace and the preferences of the tasting panel have little in common.
So, what exactly was the point of the Washington Post exercise? It may be a laudable exercise for wine writers to look at those wines that people actually drink, rather than those drunk by experts (eg. Blake Gray describes it as "outstanding service journalism"). However, we already have CellarTracker to tell us what actual wine drinkers think about the wines; and we have a bunch of specialist web sites that taste and recommend a wide range of inexpensive wines (see my post on Finding inexpensive wines). These sources can be used any time we want; we don't need a bunch of sardonic tasting notes from professionals, as well.
Personally, I would go with the CellarTracker scores, as a source of Recommended wines.
Monday, October 16, 2017
What has happened to the 1983 Port vintage?
One of the most comprehensive sites about vintage port is VintagePort.se. This site was established in 2011, by three port enthusiasts from southern Sweden. It contains details about every port brand name, and its history (with a few rare exceptions). It also contains tasting notes about nearly every vintage wine produced under those brand names, often tasted more than once — this is well over a thousand tasting notes.
Many of these ports were tasted at meetings of The Danish Port Wine Club (in Copenhagen) or The Wine Society 18% (in Malmö). Among these, there have been a few Great Tastings, during which at least 20 port brands were tasted from a particular vintage. Earlier this year it was the turn of the 1983 vintage.
The 1983 vintage was highly rated in the mid 1980s, and 36 of the houses / brands released a vintage port (ie. almost all producers declared the vintage). A survey of the vintage scores from various commentators reveals this:
So, almost all of the commentators rated the vintage as 90+, but did not rate it as among the very best of the recent Port vintages. The VintagePort.se site notes that they also previously rated the 1983 vintage as Outstanding (a score of 18 / 20 = 95).
However, earlier this year, at their Great Tasting, the three port lovers re-tasted 31 of the 36 vintage wines from 1983. They were rather disappointed: "Many wines were defective with volatile acidity, and many wines were not what we had expected ... We have now changed this vintage to the rating Very Good" (score 15 / 20 = 88). This is quite a come down.
It is now 30 years since the 1983 ports were put in their bottles. This is not usually considered to be an especially long time in the life of a vintage port, although most of this vintage has probably been consumed by now. So, what has happened to these wines? It seems unlikely that bottle variation is responsible for the poor results. Maybe the corks in use at the time were not up to he job? Or, maybe the grapes just weren't as good as people thought at the time.
The three port enthusiasts were in general agreement with each other about the scores of the 31 individual wines (although Sten and Stefan agreed more often than Jörgen), so that their group ratings were consistent.
However, it might be better if we base our overall assessment of the wines on the average score from all 16 of the participants in the Great Tasting. They rated 2 of the ports as Excellent (17 points / 20), 4 as Very fine (16 points), 17 as Very good (score 15), 4 as Good (score 14), 1 as Average (score 13), and 3 as Below average. The two best ports were from Quarles Harris and Gould Campbell, while the three worst were from Real Vinicola, Dow's and Kopke.
You can check out the full results on their site. Overall, this is quite an impressive source of information for port aficionados.
Many of these ports were tasted at meetings of The Danish Port Wine Club (in Copenhagen) or The Wine Society 18% (in Malmö). Among these, there have been a few Great Tastings, during which at least 20 port brands were tasted from a particular vintage. Earlier this year it was the turn of the 1983 vintage.
The 1983 vintage was highly rated in the mid 1980s, and 36 of the houses / brands released a vintage port (ie. almost all producers declared the vintage). A survey of the vintage scores from various commentators reveals this:
| Rating out of 100 Tom Stevenson Wine Advocate Wine Spectator Cellar Notes Into Wine MacArthur Beverages Vinous Rating out of 10 Berry Bros & Rudd Oz Clarke Vintages (LCBO) Wine Society Passionate About Port Rating out of 5 Michael Broadbent Decanter For the Love of Port |
1983 vintage 95 92 92 91 91 91 90 8 8 8 7 7 4 4 3 |
Best recent vintage 95 97 99 97 96 99 97 10 10 10 10 10 5 5 5 |
However, earlier this year, at their Great Tasting, the three port lovers re-tasted 31 of the 36 vintage wines from 1983. They were rather disappointed: "Many wines were defective with volatile acidity, and many wines were not what we had expected ... We have now changed this vintage to the rating Very Good" (score 15 / 20 = 88). This is quite a come down.
It is now 30 years since the 1983 ports were put in their bottles. This is not usually considered to be an especially long time in the life of a vintage port, although most of this vintage has probably been consumed by now. So, what has happened to these wines? It seems unlikely that bottle variation is responsible for the poor results. Maybe the corks in use at the time were not up to he job? Or, maybe the grapes just weren't as good as people thought at the time.
The three port enthusiasts were in general agreement with each other about the scores of the 31 individual wines (although Sten and Stefan agreed more often than Jörgen), so that their group ratings were consistent.
However, it might be better if we base our overall assessment of the wines on the average score from all 16 of the participants in the Great Tasting. They rated 2 of the ports as Excellent (17 points / 20), 4 as Very fine (16 points), 17 as Very good (score 15), 4 as Good (score 14), 1 as Average (score 13), and 3 as Below average. The two best ports were from Quarles Harris and Gould Campbell, while the three worst were from Real Vinicola, Dow's and Kopke.
You can check out the full results on their site. Overall, this is quite an impressive source of information for port aficionados.
Monday, October 9, 2017
Grape harvest dates and the evidence for global warming
I mentioned in my previous post (Statistical variance and global warming) that in Europe there are long-term records of the starting dates for grape harvests, and that this can be used to study changing weather patterns. This is because grape harvest dates are highly correlated with temperature — the warmer the season then the earlier will be the grape harvest. This fact has been much in the news this year, with very hot summer temperatures followed by very early grape harvests in many northern-hemisphere regions.
Written records of harvest dates exist in western Europe because the harvest dates are usually officially decreed, based on the ripeness of the grapes. The grapes are used for wine-making, and this activity has traditionally been under some sort of official control. Thus, we have historical records for many locations over many years.
I have previously shown two long-term datasets for wine-growing regions, one for Two centuries of Bordeaux vintages and one for Three centuries of Rheingau vintages. These both show very large changes in the timing of the start of the grape harvests, especially in recent decades. In this post I will look at some more data.
Much of this data has been compiled into a publicly accessible database archived at the World Data Center for Paleoclimatology (see V. Daux, I. Garcia de Cortazar-Atauri, P. Yiou, I. Chuine, E. Garnier, E. Le Roy Ladurie, O. Mestre, J. Tardaguila. 2012. An open-database of grape harvest dates for climate research: data description and quality assessment. Climate of the Past 8:1403-1418). This database comprises time series for 380 locations (see the map above), mainly from France (93% of the data) as well as from Germany, Switzerland, Italy, Spain and Luxembourg. The series have variable lengths up to 479 years, with the oldest harvest date on record being for 1354 CE in Burgundy.
Burgundy
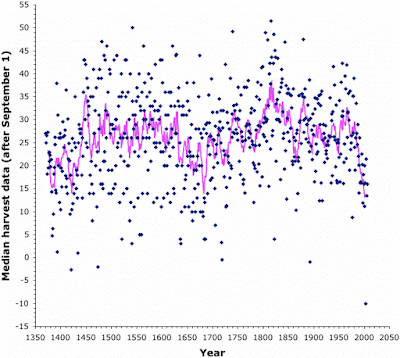
I have taken the harvest-start data for Burgundy and supplemented it with data from another study (I. Chuine, P. Yiou, N. Viovy, B. Seguin, V. Daux, E. Le Roy Ladurie. 2004. Grape ripening as a past climate indicator. Nature 432:289-290). I have graphed the data below, which shows a complete record of the official start of the grape harvest for every year from 1370 to 2006 CE, inclusive.
The harvest dates are shown relative to the beginning of September (day 0); and the pink line shows the 9-year running average.
This graph shows some very interesting patterns. First, in spite of the ups and downs in the graph, there is no long-term change — harvest starts have pretty much remained within a 4-week period after September 10.
However, the long-term pattern does show two long cycles, with harvest dates getting progressively later through time and then moving earlier again — the first cycle was from 1370 to 1700, and the second from 1700 to now. Super-imposed on these two long cycles, there were smaller 20-year cycles before 1700, and 30-year cycles after that time. For mathematicians, this might be an interesting dataset on which to perform some Fourier time-series analysis.
For our purposes here, there has been a dramatic change in harvest date in recent years, with the earlier and earlier harvests since 1984 being attributed to global warming. However, there was just as rapid a change in harvest dates from 1420 to 1450, although at that time the harvests became rapidly later, due to cooling of the weather (not warming).
This graph thus illustrates what the climate-change skeptics are on about. There have been recordings of previous large changes in the weather, which have affected European agriculture. In that sense, the current change in the weather is not necessarily unusual. The skeptics suggest that we should continue to "suck it and see", to find out whether the weather turns around and becomes cooler again. However, there have been no longer trends of change, and, unlike for the previous longest occasion, there is no current indication that our recent warming trend will reverse itself.
Australia
By way of contrast, we could also look at some shorter harvest trends from elsewhere in the world. The data I have chosen come from Australia (L.B. Webb, P.H. Whetton, E.W.R. Barlow. 2011. Observed trends in winegrape maturity in Australia. Global Change Biology 17:2707-2719).
The longest grape-maturity record presented by these authors is 115 years, for the McLaren Vale region, in South Australia. Unfortunately, the data for 1992-1997, inclusive, are missing, which reduces its utility for studying global warming.
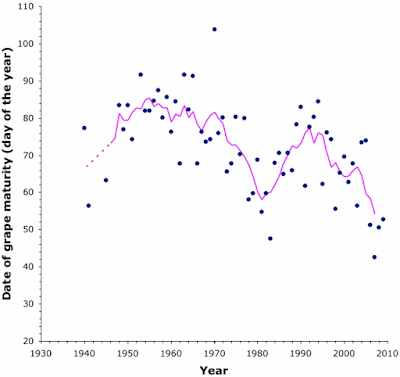
So, instead I will show the graphs for two shorter time-series from central Victoria, one for Shiraz grapes (red) and one for Marsanne (white). Note that the harvest in Australia is in March, not September. These graphs cover 70 years; and the pink lines show the 5-year running average.
Shiraz
Marsanne
The graphs both show relatively short-term cycles in grape maturity, superimposed on longer-term cycles, the same as I noted above for Burgundy. For example, for the Marsanne grapes the shorter cycles seems to be c. 20 years long. Maybe this is a common pattern for wine grapes?
In any case, the move towards earlier harvests is just as obvious in these data as it is in the data for the Burgundy region (and also for Bordeaux and the Rheingau, as shown in my earlier posts). The recent change in agriculture patterns truly is global.
The skeptics
Sadly, Australia is one of the official political homes of climate-change denial. For instance, take this comment by renowned Australian government viticulturist John Gladstones, which is from Wine, Terroir and Climate Change (Wakefield Press, 2011):
The key word in the climate debate is "prove". We cannot, in the strict sense, ever prove a causal connection between anthropogenic activities and climate change. But, by the same token, we can never prove that the sun will rise tomorrow morning, either. Both cases involve forecasts about the future, and we will only be able to evaluate them in hindsight. By then, of course, it is usually too late, if something has gone amiss.
Written records of harvest dates exist in western Europe because the harvest dates are usually officially decreed, based on the ripeness of the grapes. The grapes are used for wine-making, and this activity has traditionally been under some sort of official control. Thus, we have historical records for many locations over many years.
I have previously shown two long-term datasets for wine-growing regions, one for Two centuries of Bordeaux vintages and one for Three centuries of Rheingau vintages. These both show very large changes in the timing of the start of the grape harvests, especially in recent decades. In this post I will look at some more data.
Much of this data has been compiled into a publicly accessible database archived at the World Data Center for Paleoclimatology (see V. Daux, I. Garcia de Cortazar-Atauri, P. Yiou, I. Chuine, E. Garnier, E. Le Roy Ladurie, O. Mestre, J. Tardaguila. 2012. An open-database of grape harvest dates for climate research: data description and quality assessment. Climate of the Past 8:1403-1418). This database comprises time series for 380 locations (see the map above), mainly from France (93% of the data) as well as from Germany, Switzerland, Italy, Spain and Luxembourg. The series have variable lengths up to 479 years, with the oldest harvest date on record being for 1354 CE in Burgundy.
Burgundy
I have taken the harvest-start data for Burgundy and supplemented it with data from another study (I. Chuine, P. Yiou, N. Viovy, B. Seguin, V. Daux, E. Le Roy Ladurie. 2004. Grape ripening as a past climate indicator. Nature 432:289-290). I have graphed the data below, which shows a complete record of the official start of the grape harvest for every year from 1370 to 2006 CE, inclusive.
The harvest dates are shown relative to the beginning of September (day 0); and the pink line shows the 9-year running average.
This graph shows some very interesting patterns. First, in spite of the ups and downs in the graph, there is no long-term change — harvest starts have pretty much remained within a 4-week period after September 10.
However, the long-term pattern does show two long cycles, with harvest dates getting progressively later through time and then moving earlier again — the first cycle was from 1370 to 1700, and the second from 1700 to now. Super-imposed on these two long cycles, there were smaller 20-year cycles before 1700, and 30-year cycles after that time. For mathematicians, this might be an interesting dataset on which to perform some Fourier time-series analysis.
For our purposes here, there has been a dramatic change in harvest date in recent years, with the earlier and earlier harvests since 1984 being attributed to global warming. However, there was just as rapid a change in harvest dates from 1420 to 1450, although at that time the harvests became rapidly later, due to cooling of the weather (not warming).
This graph thus illustrates what the climate-change skeptics are on about. There have been recordings of previous large changes in the weather, which have affected European agriculture. In that sense, the current change in the weather is not necessarily unusual. The skeptics suggest that we should continue to "suck it and see", to find out whether the weather turns around and becomes cooler again. However, there have been no longer trends of change, and, unlike for the previous longest occasion, there is no current indication that our recent warming trend will reverse itself.
Australia
By way of contrast, we could also look at some shorter harvest trends from elsewhere in the world. The data I have chosen come from Australia (L.B. Webb, P.H. Whetton, E.W.R. Barlow. 2011. Observed trends in winegrape maturity in Australia. Global Change Biology 17:2707-2719).
The longest grape-maturity record presented by these authors is 115 years, for the McLaren Vale region, in South Australia. Unfortunately, the data for 1992-1997, inclusive, are missing, which reduces its utility for studying global warming.
So, instead I will show the graphs for two shorter time-series from central Victoria, one for Shiraz grapes (red) and one for Marsanne (white). Note that the harvest in Australia is in March, not September. These graphs cover 70 years; and the pink lines show the 5-year running average.
Shiraz
Marsanne
The graphs both show relatively short-term cycles in grape maturity, superimposed on longer-term cycles, the same as I noted above for Burgundy. For example, for the Marsanne grapes the shorter cycles seems to be c. 20 years long. Maybe this is a common pattern for wine grapes?
In any case, the move towards earlier harvests is just as obvious in these data as it is in the data for the Burgundy region (and also for Bordeaux and the Rheingau, as shown in my earlier posts). The recent change in agriculture patterns truly is global.
The skeptics
Sadly, Australia is one of the official political homes of climate-change denial. For instance, take this comment by renowned Australian government viticulturist John Gladstones, which is from Wine, Terroir and Climate Change (Wakefield Press, 2011):
How much warming, then, can justly be attributed to anthropogenic greenhouse gases? Taking all evidence into account, the proven amount is: none ... from a viticultural viewpoint we can conclude that any anthropogenic changes to mean temperatures will be small and, for some decades to come, unlikely to have major effects beyond those of natural climate variability.And yet, here we are, several years later, and we have already reached the limit of climate variability that we have recorded for the past 6+ centuries. How much longer are we expected to suck it and see?
The key word in the climate debate is "prove". We cannot, in the strict sense, ever prove a causal connection between anthropogenic activities and climate change. But, by the same token, we can never prove that the sun will rise tomorrow morning, either. Both cases involve forecasts about the future, and we will only be able to evaluate them in hindsight. By then, of course, it is usually too late, if something has gone amiss.
Monday, October 2, 2017
Statistical variance and global warming
The idea of global warming is a matter of meteorological record, not personal opinion. For the past quarter-century, the world's weather has been very different to the preceding half century, and this has been noted by weather bureaus around the globe.
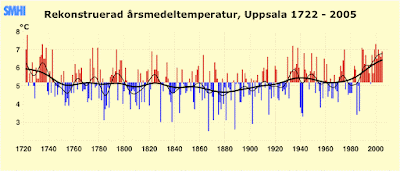
For example, the town where I live, Uppsala, has one of the longest continuous weather records in the world, starting in 1722. The recording has been carried out by Uppsala University, and the averaged data are available from its Institutionen för geovetenskaper. This graph shows the variation in average yearly temperature during those recordings, as calculated by the Swedish weather bureau (SMHI — Sveriges meteorologiska och hydrologiska institut) — red represents an above-average year and blue below-average. As you can see, below-average years have not been recorded since 1988, which is the longest run of red on record.
The consequences of this weather change have been particularly noted in agriculture, because the growth of plants is very much dependent on sunshine and rainfall — a change in either characteristic will almost certainly lead to changes in harvest quantity and quality, as well as harvest timing. (See Climate change: field reports from leading winemakers. 2016. Journal of Wine Economics 11: 5-47.)
Grape harvests
Grape harvests have been of particular interest for economic reasons, given the importance of the wine industry to many countries. However, they have also been of interest because there are many long-term harvest records for Europe, and so the changing of the harvests in response to weather conditions over several centuries has been recorded, and can be studied. I have discussed this in a post on my other blog — Grape harvest dates as proxies for global warming; and this may be of interest to you, so check it out.
I conclude that we should be in no doubt that the recent change in the weather has had a big effect on wine production, and that we can reasonably expect that this will continue while ever the current weather patterns continue.
What seems to be more contentious, however, is assessing the causes of these weather patterns, and how the people of this planet might respond, if at all. For example, Steve Heimoff, over at the Fermentation blog, has recently discussed this issue (Inconvenient timing for a climate-change heretic).
One of the important issues here is the concept of statistical variance; and this is what I will discuss in the rest of this post.
Statistical variance
"Statistical variance" refers to the variation that occurs due to random processes and stochastic events. For example, we do not expect the average yearly temperature to be the same from year to year, which is what would happen if there was no statistical variance. Instead, we have observed that each year is somewhat different, with some years being above average and some below. In the graph above, the years varied from 8°C below the long-term average to 8°C above the long-term average — these numbers quantify the amount of statistical variance that has occurred in Uppsala's weather over the past three centuries.
We also do not expect regular patterns in the statistical variance. For instance, we should be very surprised if the years always alternated between above-average and below-average temperatures. Instead, we expect runs of several years above or below, without any necessary pattern to how long those runs will be. This is precisely what is shown in the graph above, where there are runs of anywhere from 1 to 9 consecutive years with similar weather.
Importance
Human beings need to understand this concept of statistical variance in order to work out whether anything unusual is happening around them. For example, a business person needs to work out whether a run of several months of poor economic performance is simply statistical variance, or whether it indicates that something has gone wrong (and needs to be corrected). Alternatively, a run of several months of good economic performance may also be simply statistical variance, and not at all an indication that the company is being well run!
This seems to be a very hard thing for people to grasp. Runs of events, whether good or bad, are often interpreted as being non-random; and runs of apparent bad luck can be very depressing, while runs of good luck can lead to over-confidence (which is well known to come before a fall).
This topic has been discussed in a number of books. One of the better known of these is Leonard Mlodinow's 2008 book The Drunkard's Walk: How Randomness Rules Our Lives. This has a detailed discussion of "the role of randomness in everyday events, and the cognitive biases that lead people to misinterpret random events and stochastic processes." His particular message is that people who don't grasp the idea of statistical variance can be led astray by randomness — a run of bad luck does not necessarily make you a failure, nor does a run of good luck necessarily make you a success. You can watch a video presentation by him on Youtube (thanks to Bob Henry for alerting me to this).
Why we should address statistical variance
Like Mlodinow, I am particularly interested in how people respond to statistical variation.
In this context I will mention a simple example, called the Gambler's Fallacy, which is very relevant. Gambler's often think that in a game of 50:50 chance they will break even in the long term, because they will eventually win and lose the same amounts of money. However, mathematicians have shown that, due to statistical variance, this can only be guaranteed in practice if the gambler has the resources to allow for infinite gains and infinite losses (ie. they can sustain an infinitely long winning or losing streak). Such long runs of wins and losses do not result from expertise or lack of it — they will happen anyway, just by random chance. However, in practice, the gambler will stop playing when their bankroll reaches zero (from too many consecutive losses) or when they bust the casino (from too many consecutive wins). So, there is no way to guarantee to break even in the long term — either you or the casino may go bust before that happens.
The importance of this example is that it emphasizes how we deal with statistical variance, in practice. For example, in practice it does not really matter whether current climate change is a permanent change (perhaps caused by modern industrial societies) or the result of statistical variance. It will affect us either way — metaphorically, it is just as possible for either we or the casino can go bust due to statistical variance, as going bust from any other possible causes. The practical question is: what are we going to do about it? We are sentient beings (that's what our scientific name Homo sapiens means), and we thus have the ability to recognize what is happening, and to potentially do something about it. We need to decide whether we want to do something, or not.
Several decades ago, when it was pointed out that there was a hole in the ozone layer, a possible cause was identified (use of CFCs), and a potential response was outlined (stop using CFCs, because there are alternatives). We decided to respond, globally; and the latest reports show that the hole is now shrinking. Maybe the increase and decrease in the hole are simply the result of statistical variance; but maybe we are actually smarter than the skeptics think. We keep records (we describe the world), we think about the patterns observed in those records (we explain the world), and we work out how we might respond (we try to forecast the future).
However, being sentient doesn't necessarily make us intelligent. Some people are skeptics because that is how they are built; others are skeptics because they have their own agenda (often to do with them making money, and lots of it), and to hell with everything else. Intelligence requires more than skepticism; and this applies to global warming as much as anything else.
So, the skeptics are right when they point out that rapid changes in long-term weather have occurred before in our recorded history; and I will discuss the data in a future post. However, this fact is irrelevant. Our response cannot be determined by these past patterns, because the current effects are occurring now, irrespective of whether they also occurred back then. Furthermore, even if any particular climate change is "natural" doesn't mean that we will be unaffected. We are going to look like complete fools if we (metaphorically) go bankrupt while attributing it to statistical variance. This is like leaping into a deep hole while yelling "look at me, I'm falling!"
Common ways to deal with statistical variance
By way of finishing, I will mention a couple of ways that people have developed to address the effects of statistical variance. You might like to think about whether any of these can be applied to global warming.
The basic idea is to reduce the statistical variance. That is, we try to prevent long runs of positive and negative changes from happening — we reduce the extent of both the upswings and the downswings. Sadly, there is no known way to reduce the negative changes (runs of bad luck) without also reducing the positive changes (runs of good luck).
In economics and gambling, one way to do this is by hedge bets. This involves investing most of our money in one way while simultaneously investing a smaller amount in the opposite way. So, we might bet most of our money on one particular team winning the game while also placing a smaller bet on the other team. This will reduce or losses if we have put most of our money on the losing team (because we will still win the smaller bet), although it will also reduce our winnings if we have put most of our money on the winning team (because we will still lose the smaller bet). So, hedge betting reduces our possible wins and losses — that is, it reduces the statistical variance. In economics, so-called Hedge Funds operate in precisely this manner; and they seem to be quite successful financially.
A somewhat different approach is taken in card games like poker. Professional online poker players usually play hands at multiple tables simultaneously. That is, they are placing multiple bets at the same time. Each table is potentially subject to wide statistical variance, but the average across all of the tables will usually have much less variance. Across any one betting session, the losses at one table will be counter-balanced by the wins at other tables, thus reducing the statistical variance for the poker player. This is an important component of being a professional in any field — the effect of random processes (good luck and bad luck) needs to be minimized.
It might strike you as a bit odd that I am talking about gambling in terms of dealing with statistical variance, but the same principles apply to all circumstances. In practice, a poker player betting at multiple tables is mathematically no different from an insurance company having lots of policy holders — you win some and you lose some, but you will reduce the extremes of winning and losing by being involved in multiple events. Most of our understanding of the mathematics of probability has come from studying both gambling and insurance.
Mind you, often the optimal strategy in poker is to go all-in with a good hand, which means that you will immediately either double your money or go bankrupt. This is not a recommended strategy when dealing with the world as a whole!
For example, the town where I live, Uppsala, has one of the longest continuous weather records in the world, starting in 1722. The recording has been carried out by Uppsala University, and the averaged data are available from its Institutionen för geovetenskaper. This graph shows the variation in average yearly temperature during those recordings, as calculated by the Swedish weather bureau (SMHI — Sveriges meteorologiska och hydrologiska institut) — red represents an above-average year and blue below-average. As you can see, below-average years have not been recorded since 1988, which is the longest run of red on record.
The consequences of this weather change have been particularly noted in agriculture, because the growth of plants is very much dependent on sunshine and rainfall — a change in either characteristic will almost certainly lead to changes in harvest quantity and quality, as well as harvest timing. (See Climate change: field reports from leading winemakers. 2016. Journal of Wine Economics 11: 5-47.)
Grape harvests
Grape harvests have been of particular interest for economic reasons, given the importance of the wine industry to many countries. However, they have also been of interest because there are many long-term harvest records for Europe, and so the changing of the harvests in response to weather conditions over several centuries has been recorded, and can be studied. I have discussed this in a post on my other blog — Grape harvest dates as proxies for global warming; and this may be of interest to you, so check it out.
I conclude that we should be in no doubt that the recent change in the weather has had a big effect on wine production, and that we can reasonably expect that this will continue while ever the current weather patterns continue.
What seems to be more contentious, however, is assessing the causes of these weather patterns, and how the people of this planet might respond, if at all. For example, Steve Heimoff, over at the Fermentation blog, has recently discussed this issue (Inconvenient timing for a climate-change heretic).
One of the important issues here is the concept of statistical variance; and this is what I will discuss in the rest of this post.
Statistical variance
"Statistical variance" refers to the variation that occurs due to random processes and stochastic events. For example, we do not expect the average yearly temperature to be the same from year to year, which is what would happen if there was no statistical variance. Instead, we have observed that each year is somewhat different, with some years being above average and some below. In the graph above, the years varied from 8°C below the long-term average to 8°C above the long-term average — these numbers quantify the amount of statistical variance that has occurred in Uppsala's weather over the past three centuries.
We also do not expect regular patterns in the statistical variance. For instance, we should be very surprised if the years always alternated between above-average and below-average temperatures. Instead, we expect runs of several years above or below, without any necessary pattern to how long those runs will be. This is precisely what is shown in the graph above, where there are runs of anywhere from 1 to 9 consecutive years with similar weather.
Importance
Human beings need to understand this concept of statistical variance in order to work out whether anything unusual is happening around them. For example, a business person needs to work out whether a run of several months of poor economic performance is simply statistical variance, or whether it indicates that something has gone wrong (and needs to be corrected). Alternatively, a run of several months of good economic performance may also be simply statistical variance, and not at all an indication that the company is being well run!
This seems to be a very hard thing for people to grasp. Runs of events, whether good or bad, are often interpreted as being non-random; and runs of apparent bad luck can be very depressing, while runs of good luck can lead to over-confidence (which is well known to come before a fall).
This topic has been discussed in a number of books. One of the better known of these is Leonard Mlodinow's 2008 book The Drunkard's Walk: How Randomness Rules Our Lives. This has a detailed discussion of "the role of randomness in everyday events, and the cognitive biases that lead people to misinterpret random events and stochastic processes." His particular message is that people who don't grasp the idea of statistical variance can be led astray by randomness — a run of bad luck does not necessarily make you a failure, nor does a run of good luck necessarily make you a success. You can watch a video presentation by him on Youtube (thanks to Bob Henry for alerting me to this).
Why we should address statistical variance
Like Mlodinow, I am particularly interested in how people respond to statistical variation.
In this context I will mention a simple example, called the Gambler's Fallacy, which is very relevant. Gambler's often think that in a game of 50:50 chance they will break even in the long term, because they will eventually win and lose the same amounts of money. However, mathematicians have shown that, due to statistical variance, this can only be guaranteed in practice if the gambler has the resources to allow for infinite gains and infinite losses (ie. they can sustain an infinitely long winning or losing streak). Such long runs of wins and losses do not result from expertise or lack of it — they will happen anyway, just by random chance. However, in practice, the gambler will stop playing when their bankroll reaches zero (from too many consecutive losses) or when they bust the casino (from too many consecutive wins). So, there is no way to guarantee to break even in the long term — either you or the casino may go bust before that happens.
The importance of this example is that it emphasizes how we deal with statistical variance, in practice. For example, in practice it does not really matter whether current climate change is a permanent change (perhaps caused by modern industrial societies) or the result of statistical variance. It will affect us either way — metaphorically, it is just as possible for either we or the casino can go bust due to statistical variance, as going bust from any other possible causes. The practical question is: what are we going to do about it? We are sentient beings (that's what our scientific name Homo sapiens means), and we thus have the ability to recognize what is happening, and to potentially do something about it. We need to decide whether we want to do something, or not.
Several decades ago, when it was pointed out that there was a hole in the ozone layer, a possible cause was identified (use of CFCs), and a potential response was outlined (stop using CFCs, because there are alternatives). We decided to respond, globally; and the latest reports show that the hole is now shrinking. Maybe the increase and decrease in the hole are simply the result of statistical variance; but maybe we are actually smarter than the skeptics think. We keep records (we describe the world), we think about the patterns observed in those records (we explain the world), and we work out how we might respond (we try to forecast the future).
However, being sentient doesn't necessarily make us intelligent. Some people are skeptics because that is how they are built; others are skeptics because they have their own agenda (often to do with them making money, and lots of it), and to hell with everything else. Intelligence requires more than skepticism; and this applies to global warming as much as anything else.
So, the skeptics are right when they point out that rapid changes in long-term weather have occurred before in our recorded history; and I will discuss the data in a future post. However, this fact is irrelevant. Our response cannot be determined by these past patterns, because the current effects are occurring now, irrespective of whether they also occurred back then. Furthermore, even if any particular climate change is "natural" doesn't mean that we will be unaffected. We are going to look like complete fools if we (metaphorically) go bankrupt while attributing it to statistical variance. This is like leaping into a deep hole while yelling "look at me, I'm falling!"
Common ways to deal with statistical variance
By way of finishing, I will mention a couple of ways that people have developed to address the effects of statistical variance. You might like to think about whether any of these can be applied to global warming.
The basic idea is to reduce the statistical variance. That is, we try to prevent long runs of positive and negative changes from happening — we reduce the extent of both the upswings and the downswings. Sadly, there is no known way to reduce the negative changes (runs of bad luck) without also reducing the positive changes (runs of good luck).
In economics and gambling, one way to do this is by hedge bets. This involves investing most of our money in one way while simultaneously investing a smaller amount in the opposite way. So, we might bet most of our money on one particular team winning the game while also placing a smaller bet on the other team. This will reduce or losses if we have put most of our money on the losing team (because we will still win the smaller bet), although it will also reduce our winnings if we have put most of our money on the winning team (because we will still lose the smaller bet). So, hedge betting reduces our possible wins and losses — that is, it reduces the statistical variance. In economics, so-called Hedge Funds operate in precisely this manner; and they seem to be quite successful financially.
A somewhat different approach is taken in card games like poker. Professional online poker players usually play hands at multiple tables simultaneously. That is, they are placing multiple bets at the same time. Each table is potentially subject to wide statistical variance, but the average across all of the tables will usually have much less variance. Across any one betting session, the losses at one table will be counter-balanced by the wins at other tables, thus reducing the statistical variance for the poker player. This is an important component of being a professional in any field — the effect of random processes (good luck and bad luck) needs to be minimized.
It might strike you as a bit odd that I am talking about gambling in terms of dealing with statistical variance, but the same principles apply to all circumstances. In practice, a poker player betting at multiple tables is mathematically no different from an insurance company having lots of policy holders — you win some and you lose some, but you will reduce the extremes of winning and losing by being involved in multiple events. Most of our understanding of the mathematics of probability has come from studying both gambling and insurance.
Mind you, often the optimal strategy in poker is to go all-in with a good hand, which means that you will immediately either double your money or go bankrupt. This is not a recommended strategy when dealing with the world as a whole!
Subscribe to:
Posts (Atom)